Certainly not as early as Columbus sailed around the globe. The first person to suggest that the earth should have a spherical shape was the Greek mathematician Pythagoras, and later the Greek philosopher Aristotle explained in practical terms why the earth should be spherical. During the eclipse, Aristotle realized that the earth was between the moon and the sun, and that in each eclipse the earth’s shadow on the moon was always circular. Aristotle believed that if the earth were a large circle, as many people are saying, it should be in a straight circle only when the sun was shining directly on it, and when it was tilted, it should be elongated.
However, Aristotle argued that since every lunar eclipse, the earth’s shadow was always circular, the circle was round, and that no matter what angle the sun shone on it, the earth’s shadow must be circular. Aristotle also noticed that the orbits of stars were different in different parts of the world. Therefore, based on these two considerations, Aristotle concluded that the earth is not just a circle but a sphere. In fact, his ideas were 100% correct. When we look at the stars around the equator, we can see that the stars are moving in a straight line from east to west, and in the polar regions we can see that the stars are moving in a circular motion.
Another Greek mathematician, Eratosthenes, proved that the earth was spherical. He, like Leonardo da Vinci, was a versatile man, and he was an astronomer. Math He is also an expert in geography and philosophy. Not only did he prove that the earth was round, but he could also measure the circumference of the earth using sticks and the shadow of the sun. Arotos Thanes was so eager to create a world map that he first needed to know the size of the earth.
He lives in Alexandria, now Egypt, near the Nile. When he saw a well in Syene, at noon the sun’s shadow struck the well and saw no shadow outside. So when he returned to his hometown of Alexandria, he performed an experiment similar to that of the well. He planted a stick on the ground and studied the shadow of the stick. By noon, when the sun was setting on a well in Sydney, the shadow of a stick in his hometown of Alexandria was slightly northerly.
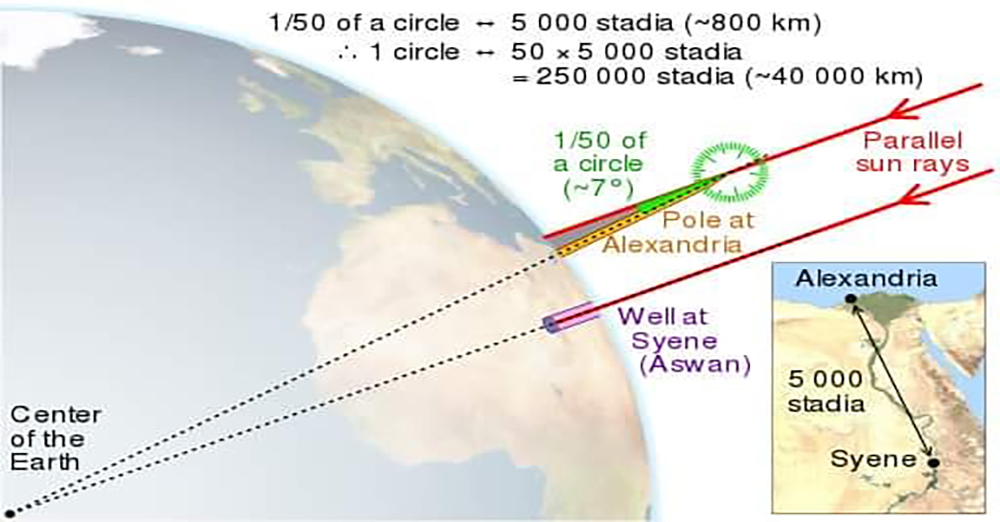
When the edge of the emerging shadow and the end of the stick were pulled by the rope, the top of the resulting triangle was 7.2 degrees. The reason for this shadow is that the city of Alexandria is located north of the equator north of the Earth. The city of Saigon, which now has no shadow from the well, is located very close to the equator. But in hindsight, that’s not the case. This is because a person who is just thinking will easily conclude that the shadow is coming from the side of the sun, not in the middle. But the problem is not that simple.
Because the sun is many times bigger than the earth. Even if the sun were thought to be smaller than the earth at that time due to a lack of knowledge, its size would still be quite large, and its light would surely fall directly on the earth. In order for a shadow to form, the path of the light source must be tilted. Otherwise, the light-receiving card must be tilted. So now that the light source is not tilted, the only thing that remains is the tilt that accepts the light.
At this point, the earth’s surface is tilted, as it were, like a plate that receives light. It is important to note that the world is not tilted at this point because the shadow does not come out on either side of the well in Saigon. But in Alexandria, farther from the equator than in Ceylon, the shadow is moving north, and the earth is tilted north. So what’s happening as the world tilts? So the surface of the earth is definitely curved. For one thing, the stick may have been tilted, and the ground may have been tilted. But mathematicians are not so bad. He believed that the scales and water scales had existed since their time, so he believed that they were accurate.
So let me tell you how he came up with the idea. At present, the city of Saigon, where there is no shadow well, and the city of Alexandria, which has a shady cane, are 5,000 stadia apart. “Stadia” is an ancient Greek unit of measurement, and 5000stadia is 800 km or 497 miles away. The upper right angle of the triangle, which now extends from the shadow to the rod, is 7.2 ° (7.2 °). To be a circle you need to be 360 degrees, so 7.2 degrees is one-fifth of a circle.
Thus, the distance of 800 km between the two cities would automatically become a circumference of one-fifth of the total circumference. So to complete the whole circle, we now need 50 circles of 800 kilometers. To be clear. Since a circle has 360 degrees, 360 degrees is 50 times 7.2 degrees. So to get a 360-degree circle, you now need to combine 50 of the 7.2-degree circles. Each of these 7.2-degree circles has a circumference of 800 km, so if we add 50 of these circles, we now have a full circle. So 50 times 80 kilometers is equal to 40,000 kilometers, so his total circumference is 40,000 kilometers (it would be easier to understand if you look at the first picture below).
The answer that came out of this simple calculation was incredibly close. Today, the circumference of the Earth is measured around the equator at 4,075 km, and the circumference of the Earth is measured at 4,008 km at both poles. Therefore, the theory of measurement by Arthur Tennys, who was able to calculate the most accurate results at that time, was really technologically advanced and absolutely accurate.
So in my opinion, he’s a little bit wrong when it comes to measuring the vertex of the triangle. Everyone knows that degrees are used as units of angles when measuring angles. This degree is divided into 60 minutes at 1 degree, and that minute is divided into 60 seconds. So even if he missed one second at 3,600 degrees 1 degree when he measured the angle, he would have missed more than 11 kilometers around the globe, and now he’s missed more than 70 kilometers at 6 seconds.
Six seconds is only one-sixth of 600 degrees, which is insignificant in normal cases, but it can cause miles of misalignment when measuring the circumference of an object as large as Earth. However, even in his day, measurements were accurate to degrees and minutes, and careful measurements of “7 degrees, 12 minutes” (7.2 °) were obtained. If its triangular measurements were misaligned by 6 seconds, it would be about one-half to one-tenth of a degree. Even a two-minute accident can take thousands of miles around the globe. Therefore, except for just six seconds, which is one hundredth of a 600th of a degree measurement, the accuracy of the Earth’s circumference was only 74 kilometers (45 miles), which is unbelievably accurate in his day. It’s so brilliant.